Periodicamente durante la pandemia di Covid-19, il personale scientifico del CDC ha utilizzato i dati dei propri studi disponibili per stimare l’efficacia delle versioni attuali o recenti dei vaccini Covid-19 per ridurre il rischio di risultare positivi al Covid-19. Sebbene il fatto di “risultare positivo” sia stato alquanto controverso a causa dei numeri soglia segreti PCR Ct coinvolti che hanno consentito a persone non infette con Covid-19 non riconosciuto da alcune settimane di rimanere positive al test, il mio obiettivo qui è quello di illustrare I problematici metodi epidemiologici del CDC che hanno sostanzialmente gonfiato le percentuali di efficacia del vaccino da loro riportate.
Gli studi epidemiologici controllati rientrano in tre e solo tre disegni di studio di base. Viene campionato un campione totale di soggetti e ciascun soggetto viene valutato sia per lo stato del caso che per lo stato dell'esposizione precedente (si tratta di uno studio trasversale) oppure vengono seguiti un campione di persone esposte e un campione di persone non esposte per vedere chi diventa un caso e da chi viene ottenuto un controllo (uno studio di coorte) o un campione di casi e un campione di controlli e ciascun soggetto viene valutato per lo stato di esposizione passata: questo è uno studio caso-controllo. Se uno studio di coorte prevede la randomizzazione dei soggetti in esposti e non esposti, si tratta di uno studio randomizzato e controllato (RCT), ma il disegno dello studio è ancora di coorte.
In uno studio trasversale e in uno studio di coorte, il rischio di ottenere l'esito di interesse (cioè, di essere un soggetto del caso, in questo caso, risultando positivo) può essere stimato per le persone esposte dal numero di casi tra gli esposti diviso per il numero totale degli esposti. Allo stesso modo per i non esposti. Ciò che è interessante, il confronto di questi due rischi, il rischio relativo (RR), è il rischio degli esposti diviso per il rischio dei non esposti. Il RR stima quanto sia peggiore il rischio tra gli esposti rispetto ai non esposti. Per un vaccino o altra esposizione che riduce il rischio, il RR sarà inferiore a 1.0.
Gli studi trasversali e di coorte, attraverso i loro disegni di campionamento, consentono di stimare il RR a partire dai loro dati. Tuttavia, gli studi caso-controllo non consentono di stimare i rischi di esito, poiché la modifica del numero relativo di casi campionati rispetto ai controlli influisce su quali sarebbero le stime del rischio. Invece, gli studi caso-controllo consentono la stima del probabilità del risultato, non del rischio. Ad esempio, probabilità 2:1 che un evento accada. Questo valore non è influenzato dal disegno di campionamento. Negli studi caso-controllo, la probabilità relativa (o odds ratio, OR) del risultato è stimata dalla probabilità del risultato tra gli esposti, divisa per la probabilità tra i non esposti.
Per un vaccino, la sua efficacia è stimata pari a 1.0 – RR. Per i dati di studi caso-controllo che stimano solo l'OR e non l'RR, quando l'OR approssima l'RR in modo sufficientemente accurato da poter essere sostituito in questa formula? Questa domanda ha una storia epidemiologica dettagliata che va oltre l’ambito attuale, ma nel senso più semplice, l’OR si avvicina all’RR quando nella popolazione i casi sono poco frequenti rispetto ai controlli.
Passiamo ora al CDC e ai suoi errori epidemiologici sistematici. In una recente analisi, Link-Gelles e colleghi hanno campionato un totale di 9,222 individui sintomatici idonei al Covid-19 che richiedevano il test Covid-19 presso le farmacie CVS e Walgreen Co. dal 21 settembre 2023 al 14 gennaio 2024. Hanno valutato il precedente stato vaccinale di ciascun individuo, nonché la positività del risultato del test. Per definizione, questo è uno studio trasversale, perché i singoli numeri di casi e controlli, o i singoli numeri di esposti (vaccinati) e non esposti (non vaccinati) non sono stati campionati. È stato campionato solo il numero totale di soggetti.
Tuttavia, i ricercatori hanno stimato l’OR e non l’RR da questi dati, utilizzando un metodo di analisi statistica chiamato regressione logistica che consente di aggiustare l’OR per vari possibili fattori confondenti. Non c’è niente di sbagliato nell’utilizzare la regressione logistica e nell’ottenere OR stimati in qualsiasi disegno di studio; il problema è utilizzare il valore OR anziché RR nella formula di efficacia del vaccino 1.0 – RR. Poiché il disegno dello studio era trasversale, i ricercatori avrebbero potuto esaminare la presenza relativa dei casi nella popolazione in base ai numeri campionati, ma non sembra che lo abbiano fatto. In effetti, i casi comprendevano 3,295 dei 9,222 totali campionati, il 36%, che non è abbastanza piccolo da utilizzare l'OR come sostituto dell'RR. Ciò vale sia tra gli esposti (25%) che tra i non esposti (37%).
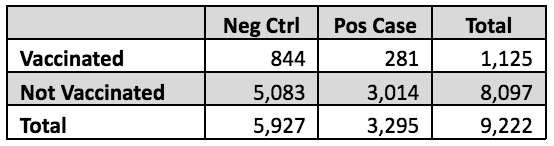
Tuttavia, è possibile avere un’idea approssimativa di quanto questa cattiva ipotesi abbia influito sull’efficacia complessiva del vaccino dichiarata dagli autori, pari al 54%. I numeri rilevanti di soggetti, mostrati nella tabella seguente, sono indicati nelle tabelle 1 e 3 del documento Link-Gelles. Il calcolo RR da questi dati grezzi è semplice. Il rischio nei vaccinati è 281/1,125 = 25%; nei non vaccinati è 3,014/8,097 = 37%. Il RR è il rapporto tra questi due, 25%/37% = 0.67, quindi l’efficacia del vaccino basata su questi dati grezzi sarebbe 1.0 – 0.67 = 0.33 o 33%.
Allo stesso modo l’OR può essere stimato da questi dati grezzi come 0.56, che se utilizzato nella formula di efficacia del vaccino darebbe un’efficacia del 44%, sensibilmente diversa dall’efficacia del 33% adeguatamente stimata utilizzando l’RR.
Tuttavia, Link-Gelles et al. hanno utilizzato l'OR corretto = 0.46 ottenuto dalla loro analisi di regressione logistica. Ciò differisce dall'OR non corretto = 0.56 di un fattore pari a 0.46/0.56 = 0.82. Possiamo utilizzare questo fattore di aggiustamento, 0.82, per approssimare quale sarebbe stato il RR grezzo se fosse stato aggiustato dagli stessi fattori: 0.67*0.82 = 0.55. Questi numeri sono mostrati nella tabella seguente e dimostrano che l’efficacia corretta del vaccino è circa il 45%, non il 54% dichiarato e inferiore al livello desiderato nominale del 50%.

Come epidemiologo, non mi è chiaro il motivo per cui i miei colleghi del CDC avrebbero erroneamente utilizzato l’OR come sostituto dell’RR quando il presupposto richiesto per questa sostituzione non era stato soddisfatto ed era facilmente verificabile nei loro dati. Hanno commesso questo errore altrove (Tenforde et al.) dove ha anche apportato una differenza considerevole nell'efficacia del vaccino, circa il 57% rispetto all'82% dichiarato. Forse gli autori pensavano che l’unico metodo disponibile per correggere molteplici variabili di confondimento fosse la regressione logistica che utilizza l’OR, ma la regressione del rischio relativo per correggere l’RR è disponibile da tempo in vari pacchetti di analisi statistica commerciale ed è facilmente implementabile (ginepro).
Mi sembra sorprendente che apparentemente nessuno degli oltre 60 autori tra gli articoli di Link-Gelles e Tenforde abbia riconosciuto che il disegno di campionamento dei loro studi era trasversale, non caso-controllo, e quindi che il parametro corretto da utilizzare per la stima l’efficacia del vaccino era l’RR e non l’OR e che l’ipotesi di una malattia rara per la sostituzione dell’OR con l’RR non era soddisfatta nei loro dati. Questi studi hanno quindi sostanzialmente sovrastimato la vera efficacia del vaccino nei loro risultati. Questa non è una questione puramente accademica, perché le decisioni di politica sanitaria pubblica del CDC possono derivare da risultati errati come questi.
Pubblicato sotto a Licenza internazionale Creative Commons Attribution 4.0
Per le ristampe, reimpostare il collegamento canonico all'originale Istituto di arenaria Articolo e Autore.









